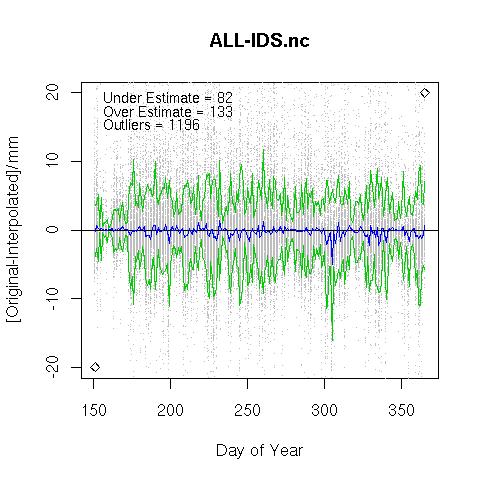
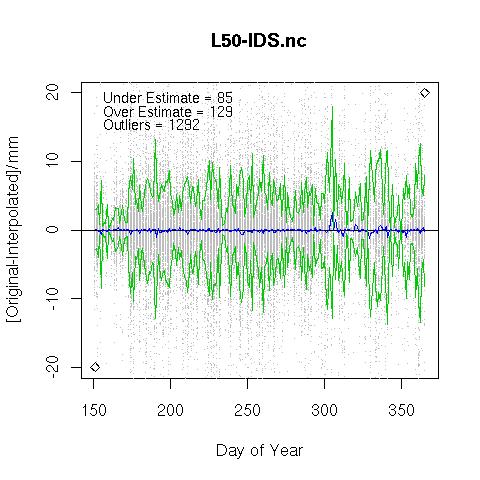
Inverse Distance Squared
☚ WORKING
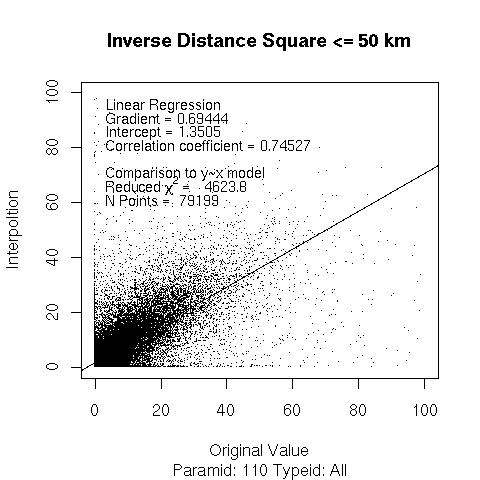
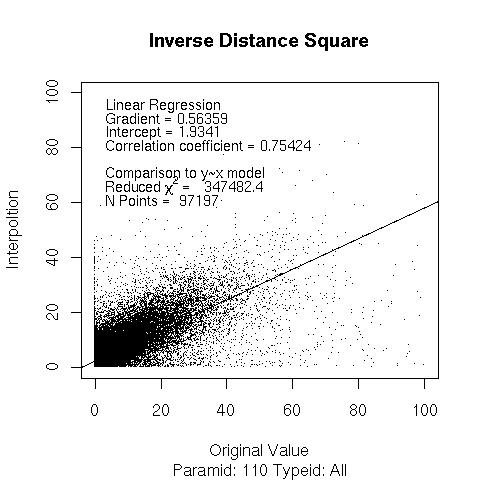
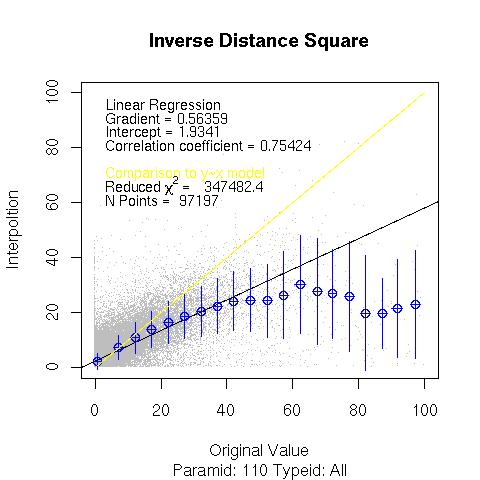
Data from 2007.05.31 to 2007.12.31. For every observed value of 24 hour precipitation at a station a model value is calulated at the same point performing an inverse distance squared weighted interpolation over the nearest neighbours.
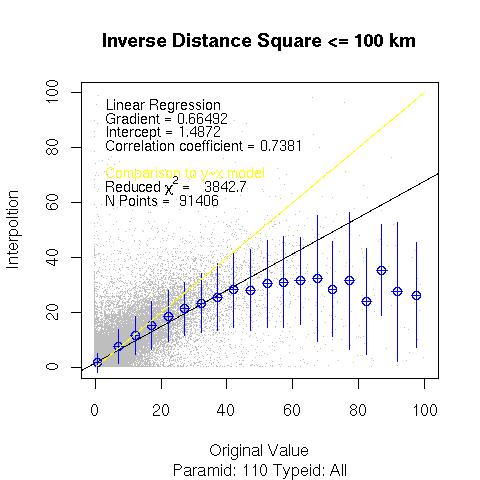
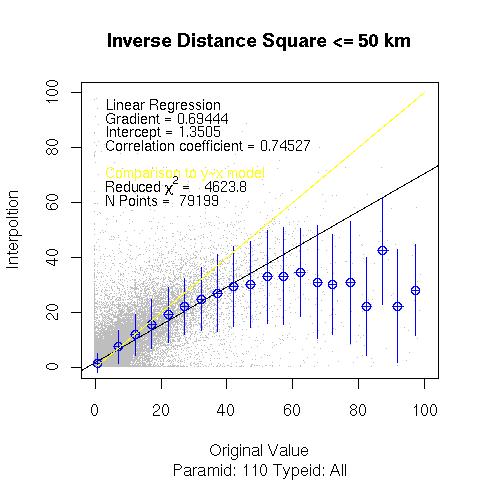
Interpolated_Value = SUM[Neighbour_Value/(D*D)] / SUM[ 1/(D*D)]
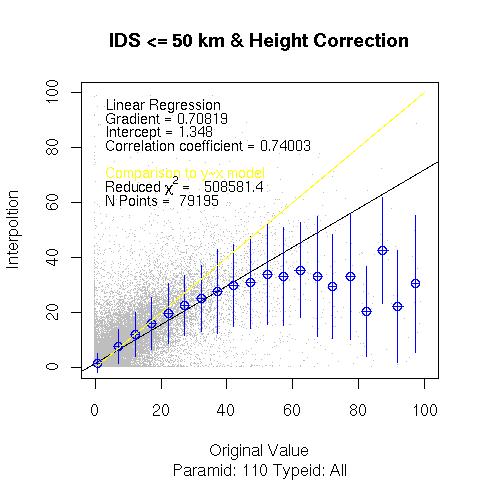
D : The distance between the modeled point and the neighbour station. The sum is performed over only the neighbours lieing within 50 km of the model point. The graph below depicts the interpolated value at the model point against the actual observed value at that station.
The same algorithm is applied below but with all neighbours within 100 km distance.
… and if no range limit is applied (i.e. interpolate over all possible neighbours).
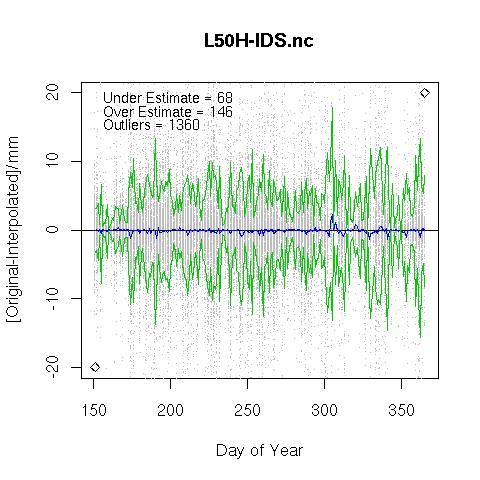
Inverse Distance Squared (with Height Correction)
The same algorithm is applied as for normal inverse distance square weighting except that all observations are reduced to a modelled value at sea-level, the interpolation is performed, and the result is scaled back to the interpolated point real altitude. For all altitudes below 1000 m the precipitation value decreases by 10% per 100m altitude, above 1000m the change is 5% per 100m.
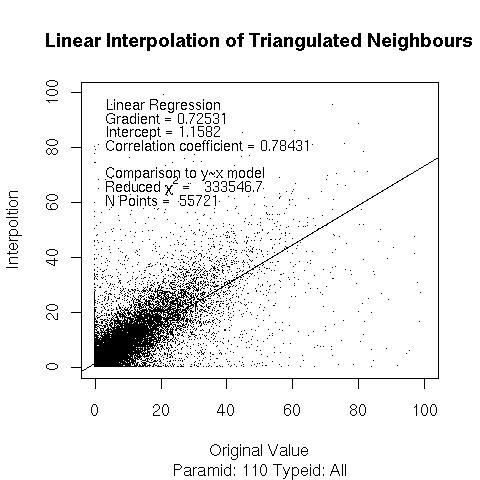
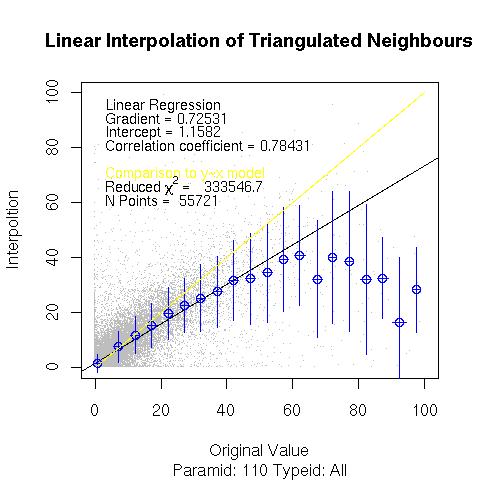
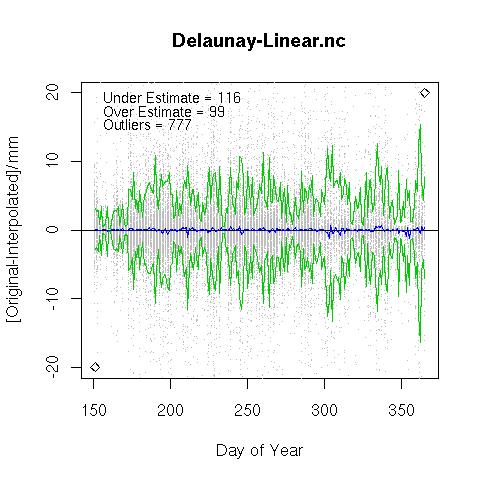
Linear Interpolation over neighbours selected by Delaunay Interpolation
For a given point all neighbours with valid measurements (i.e. no missing values) are analyzed. A Delaunay Triangulation is applied to find the best three neighbours corresponding to the point of interest (e.g. Delaunay Example) and the constraint of fitting triangles to all the stations in the neighbourhood. The neighbourhood is constrained to be a limited number of stations that lie within a fixed distance of point of interest (e.g. 50 km in the example below).
Linear interpolation is then performed as follows (details courtesy of MM).
Denom=(x3-x1)*(y2-y1)-(x2-x1)*(y3-y1) d_rr_over_d_x=((y2-y1)*(rr3-rr1)-(y3-y1)*(rr2-rr1))/Denom d_rr_over_d_y=((x3-x1)*(rr2-rr1)-(x2-x1)*(rr3-rr1))/Denom rr=rr1+(x-x1)*d_rr_over_d_x+(y-y1)*d_rr_over_d_y
where x1, x2, x3 and y1, y2, y3 are the x and y coordinates of the three points of the triangle of interest. x and y are the coordinates of the point where RR is to be calculated. rr is the calculated precipitation.
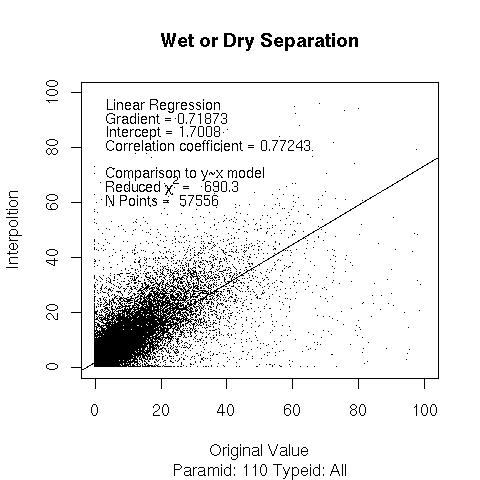
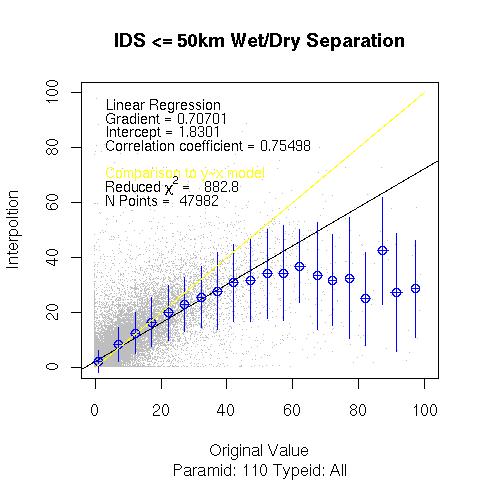
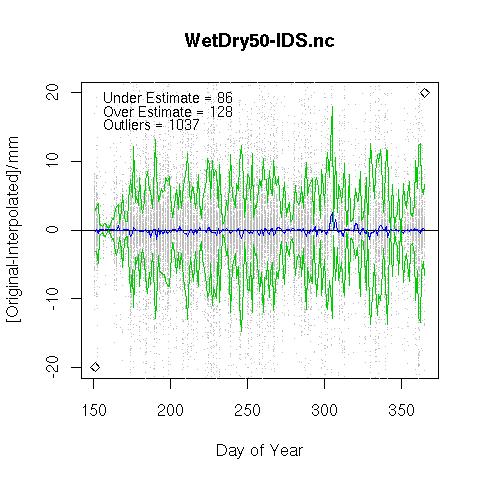
Wet or Dry Separation
Sanity Check
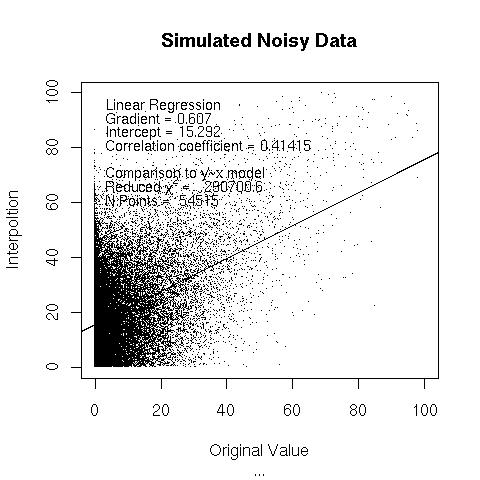
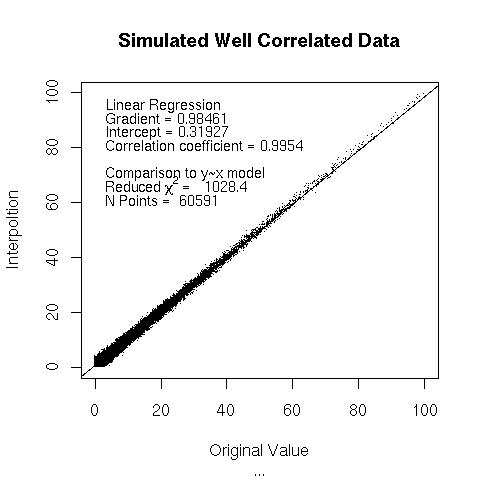
The following graphs includes simulated data to check the validity of the statistical values encoded.